Potenciação No Dia A Dia Exemplos – Potenciação No Dia a Dia: Exemplos e Aplicações desvenda o poder da potenciação, uma operação matemática fundamental que permeia diversos aspectos da nossa vida. A potenciação, que consiste em multiplicar um número por si mesmo um determinado número de vezes, é uma ferramenta essencial para a compreensão de fenômenos como crescimento exponencial, cálculos financeiros e até mesmo a descrição de processos físicos.
Neste artigo, exploraremos o conceito de potenciação, suas propriedades e aplicações práticas em cenários reais, desvendando como essa operação matemática molda o mundo ao nosso redor.
Potenciação na Vida Diária: Potenciação No Dia A Dia Exemplos
A potenciação é uma operação matemática fundamental que desempenha um papel crucial em diversas áreas da nossa vida, desde as finanças até a tecnologia e as ciências. Ela representa a multiplicação repetida de um número por ele mesmo, um número específico de vezes.
Conceito de Potenciação
A potenciação é representada por uma base e um expoente. A base é o número que será multiplicado por si mesmo, enquanto o expoente indica quantas vezes a base será multiplicada. Por exemplo, 2 3significa 2 multiplicado por si mesmo 3 vezes, resultando em 2 x 2 x 2 = 8.
Comparando a Potenciação com Outras Operações
A potenciação se diferencia das outras operações matemáticas básicas, como adição, subtração, multiplicação e divisão, pelo seu caráter exponencial. Enquanto a adição e a subtração envolvem a combinação ou a remoção de quantidades, a multiplicação representa a soma repetida de um número, e a divisão representa a divisão de um número em partes iguais, a potenciação envolve a multiplicação repetida de um número por si mesmo.
Aplicações da Potenciação na Vida Diária
A potenciação tem aplicações diversas em áreas como:
Finanças
A potenciação é fundamental para calcular juros compostos, onde o valor do investimento aumenta exponencialmente ao longo do tempo. Por exemplo, se você investir R$ 1.000 a uma taxa de juros anual de 10%, após 5 anos, seu investimento terá crescido para R$ 1.610,51, usando a fórmula: 1000 x (1 + 0.10) 5.
Tecnologia
A potenciação é utilizada em diversas áreas da tecnologia, como na computação gráfica, onde é aplicada para criar efeitos visuais e animações complexas. Em redes de computadores, a potenciação é usada para calcular o número de conexões possíveis entre dispositivos.
Ciências
A potenciação é aplicada em diversas áreas da ciência, como física, química e biologia. Na física, a potenciação é usada para calcular a energia cinética de um objeto, que é proporcional ao quadrado da sua velocidade. Na química, a potenciação é usada para calcular a concentração de uma solução, que é proporcional ao número de moléculas dissolvidas em um determinado volume.
Aplicações da Potenciação em Cenários Reais

A potenciação, apesar de parecer um conceito matemático abstrato, está presente em diversas situações do nosso dia a dia, influenciando desde o crescimento de investimentos até a força de um objeto em movimento. A compreensão da potenciação nos permite analisar e prever como grandezas variam em diferentes cenários.
Aplicações da Potenciação em Diferentes Áreas
A tabela a seguir ilustra exemplos de como a potenciação é utilizada em diferentes áreas da vida:
| Área | Exemplo | Fórmula matemática | Resultado |
|---|---|---|---|
| Finanças | Cálculo de juros compostos em um investimento de R$ 1.000,00 a uma taxa de 10% ao ano, durante 5 anos. | A = P(1 + i)^n | A = 1000(1 + 0,1)^5 = R$ 1.610,51 |
| Biologia | Cálculo do crescimento de uma população de bactérias que dobra a cada hora, partindo de 100 bactérias. | P(t) = P0
|
P(5) = 100
|
| Tecnologia | Estimação da capacidade de armazenamento de um disco rígido de 1 terabyte (1 TB = 1024 GB). | 1 TB = 1024 GB = 1024
|
1 TB = 1.099.511.627.776 bytes |
| Física | Cálculo da energia cinética de um carro de 1000 kg com velocidade de 20 m/s. | Ec = (1/2)
|
Ec = (1/2)
|
Exemplos de Aplicações da Potenciação no Dia a Dia
A potenciação está presente em diversas situações do nosso dia a dia, como:
- Cálculo de juros compostos em investimentos:Os juros compostos são calculados sobre o valor inicial do investimento mais os juros acumulados em períodos anteriores. A fórmula para calcular juros compostos é: A = P(1 + i)^n, onde A é o montante final, P é o principal, i é a taxa de juros e n é o número de períodos.
Por exemplo, se você investir R$ 1.000,00 a uma taxa de 10% ao ano, durante 5 anos, o montante final será de R$ 1.610,51.
- Determinação do crescimento populacional:O crescimento populacional pode ser modelado utilizando a fórmula P(t) = P0 – (1 + r)^t, onde P(t) é a população no tempo t, P0 é a população inicial, r é a taxa de crescimento e t é o tempo.
Por exemplo, se a população de uma cidade é de 100.000 habitantes e cresce a uma taxa de 2% ao ano, a população após 10 anos será de aproximadamente 121.900 habitantes.
- Estimação da capacidade de armazenamento de dados em computadores:A capacidade de armazenamento de dados em computadores é medida em bytes, kilobytes, megabytes, gigabytes, terabytes, etc. Cada unidade é 1024 vezes maior que a anterior. Por exemplo, um disco rígido de 1 terabyte (1 TB) tem uma capacidade de armazenamento de 1.099.511.627.776 bytes.
- Cálculo da energia cinética de um objeto em movimento:A energia cinética de um objeto em movimento é dada pela fórmula Ec = (1/2) – m – v^2, onde Ec é a energia cinética, m é a massa do objeto e v é a velocidade. Por exemplo, um carro de 1000 kg com velocidade de 20 m/s tem uma energia cinética de 200.000 Joules.
Potenciação e suas Propriedades
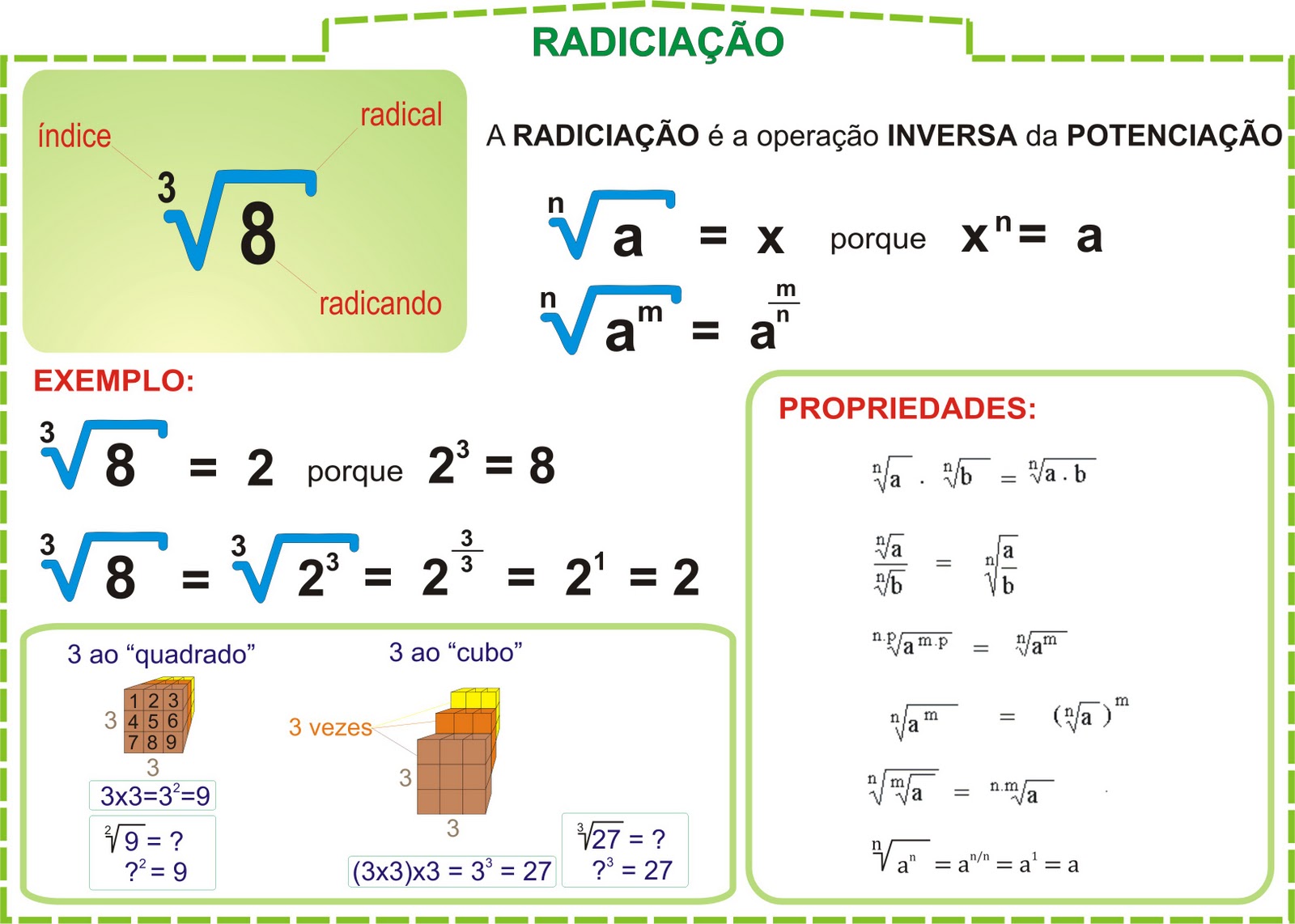
A potenciação é uma operação matemática fundamental que representa a multiplicação repetida de um número por ele mesmo. As propriedades da potenciação facilitam a manipulação de expressões matemáticas, simplificando cálculos e tornando a resolução de problemas mais eficiente.
Multiplicação de potências com mesma base
Quando multiplicamos potências com a mesma base, conservamos a base e somamos os expoentes.
am. a n= a m+n
Exemplo: 3. 2 4= 2 3+4= 2 7
Divisão de potências com mesma base
Ao dividir potências com a mesma base, mantemos a base e subtraímos os expoentes.
am/ a n= a m-n
Exemplo:
5/ 3 2= 3 5-2= 3 3
Potenciação de uma potência
Para elevar uma potência a outra potência, mantemos a base e multiplicamos os expoentes.
(am) n= a m.n
Exemplo:(5 2) 3= 5 2.3= 5 6
Potenciação de um produto
Para elevar um produto a uma potência, elevamos cada fator do produto à potência.
(a . b)n= a n. b n
Exemplo:(2 . 3) 4= 2 4. 3 4
Potenciação de um quociente
Para elevar um quociente a uma potência, elevamos o numerador e o denominador à potência.
(a / b)n= a n/ b n
Exemplo:(4 / 2) 3= 4 3/ 2 3
A potenciação, uma operação matemática aparentemente simples, revela-se um conceito poderoso com aplicações vastas e profundas em diversos campos. Desde o cálculo de juros compostos até a modelagem de fenômenos naturais, a potenciação permite compreender e quantificar o mundo de forma mais precisa.
Ao dominar os princípios da potenciação e suas propriedades, adquirimos uma ferramenta essencial para a análise e resolução de problemas em diferentes áreas do conhecimento.

