Exemplos De Análise Combinatória No Dia A Dia: Desvendando Possibilidades Inimagináveis. A análise combinatória, uma ferramenta matemática poderosa, oferece insights valiosos sobre as inúmeras maneiras pelas quais escolhas e arranjos afetam nossas vidas diárias.
Desde combinar roupas até escolher pratos em um menu, organizar livros e até mesmo distribuir prêmios em sorteios, a análise combinatória nos ajuda a quantificar e compreender a amplitude de opções disponíveis para nós.
Combinações de roupas
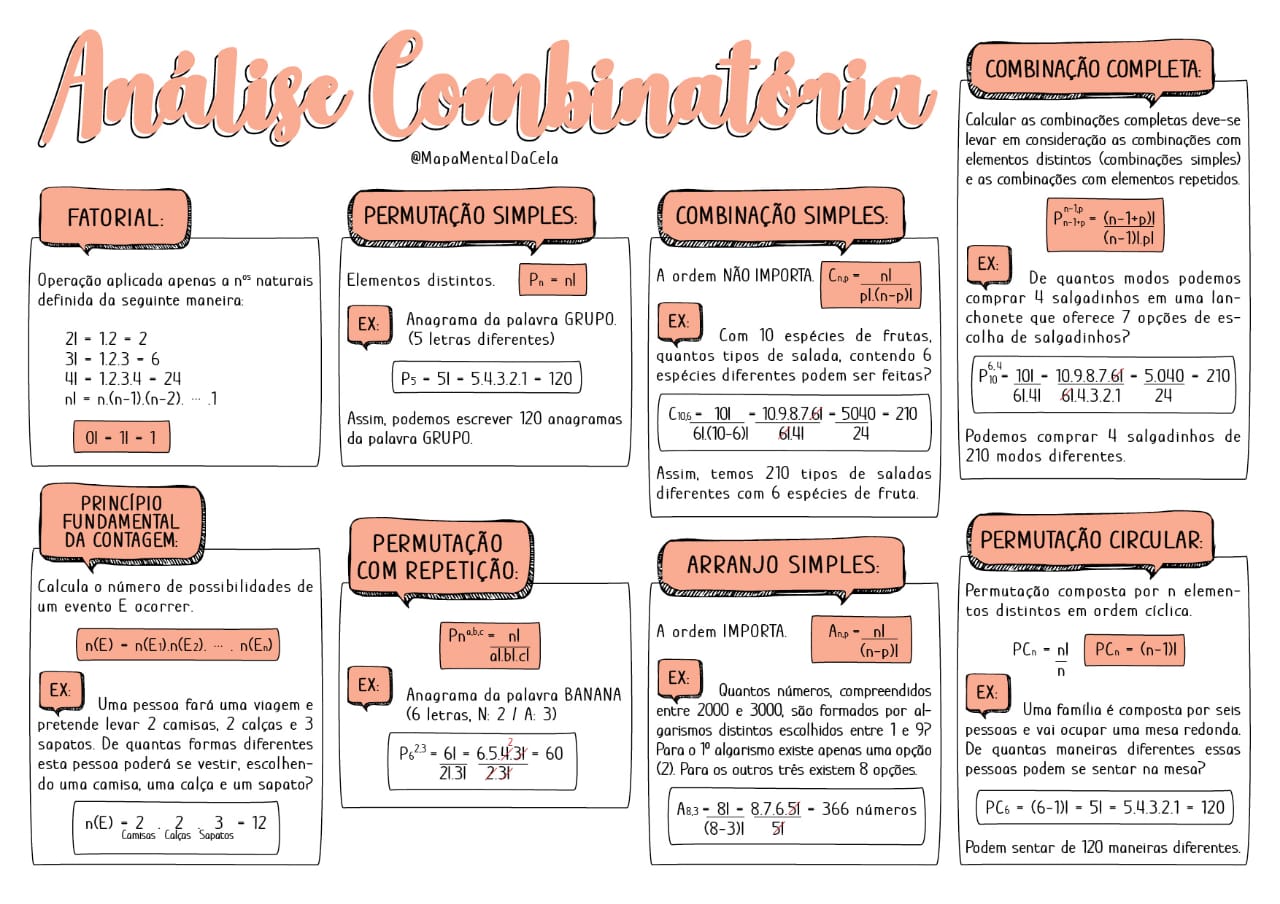
A análise combinatória pode ser usada para determinar o número de combinações de roupas possíveis em um guarda-roupa. Por exemplo, se você tem 5 camisas, 3 calças, 2 sapatos e 4 acessórios, o número de combinações possíveis é:
x 3 x 2 x 4 = 120
Isso significa que você tem 120 opções diferentes de roupas para escolher todos os dias.A tabela abaixo mostra o número de opções disponíveis para cada peça de roupa:| Peça de roupa | Número de opções ||—|—|| Camisas | 5 || Calças | 3 || Sapatos | 2 || Acessórios | 4 |
Escolha de pratos em um menu
A análise combinatória também é útil na hora de escolher pratos em um menu. Com ela, é possível calcular o número de maneiras diferentes de combinar entradas, pratos principais, acompanhamentos e sobremesas, considerando as opções disponíveis para cada categoria.
Exemplo
Considere um menu com as seguintes opções:
| Entradas | Pratos principais | Acompanhamentos | Sobremesas |
|---|---|---|---|
| 3 | 5 | 4 | 2 |
Para calcular o número total de maneiras de escolher um prato de cada categoria, multiplicamos o número de opções de cada uma:“`
(entradas) x 5 (pratos principais) x 4 (acompanhamentos) x 2 (sobremesas) = 120
“`Portanto, existem 120 maneiras diferentes de escolher um prato completo nesse menu.
Organização de livros em uma estante
A análise combinatória pode auxiliar na determinação do número de maneiras possíveis de organizar livros em uma estante com diferentes alturas e larguras. Cada livro pode ser considerado um elemento distinto, e as diferentes posições na estante podem ser vistas como espaços vazios.
Tamanhos e posições dos livros
Suponha que tenhamos uma estante com 4 prateleiras, cada uma com capacidade para 3 livros. Além disso, temos 6 livros de tamanhos variados, conforme mostrado na tabela abaixo:
| Livro | Altura | Largura |
|---|---|---|
| A | 20 cm | 15 cm |
| B | 25 cm | 18 cm |
| C | 18 cm | 12 cm |
| D | 22 cm | 16 cm |
| E | 16 cm | 10 cm |
| F | 23 cm | 17 cm |
Sequências de números

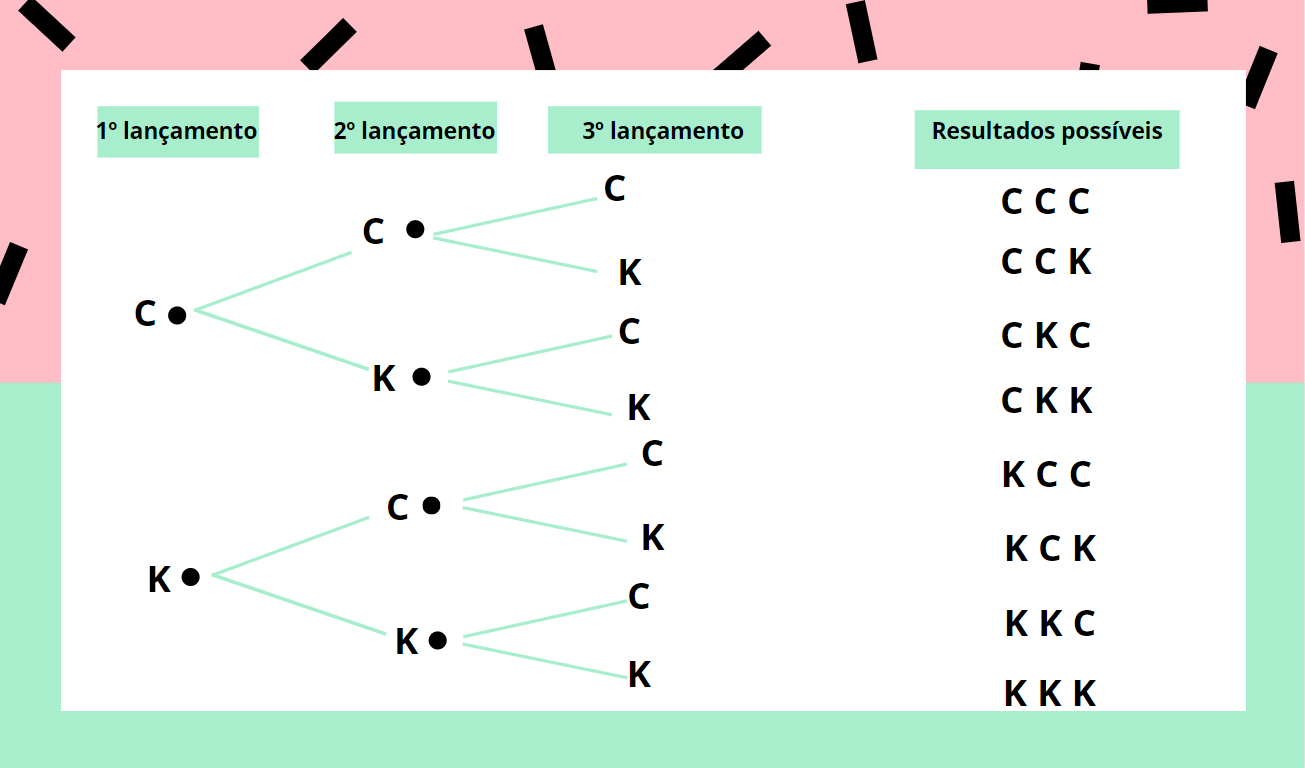
A análise combinatória pode ser usada para calcular o número de sequências de números possíveis que atendem a certos critérios. Por exemplo, podemos calcular o número de sequências de três dígitos que podem ser formadas usando os dígitos 1, 2, 3 e 4, sem repetições.
Sequências de três dígitos, Exemplos De Análise Combinatória No Dia A Dia
- Dígitos: 1, 2, 3, 4
- Tamanho da sequência: 3
- Número de combinações possíveis: 4 3= 64
Podemos calcular o número de sequências de quatro dígitos que podem ser formadas usando os dígitos 0, 1, 2, 3, 4 e 5, permitindo repetições.
Sequências de quatro dígitos com repetições
- Dígitos: 0, 1, 2, 3, 4, 5
- Tamanho da sequência: 4
- Número de combinações possíveis: 6 4= 1296
A análise combinatória pode ser usada para resolver uma ampla variedade de problemas envolvendo sequências de números. Esses problemas podem surgir em diversas áreas, como matemática, ciência da computação e estatística.
Distribuição de prêmios em um sorteio: Exemplos De Análise Combinatória No Dia A Dia
A análise combinatória pode ser usada para determinar o número de maneiras diferentes de distribuir prêmios em um sorteio com vários vencedores. Isso é importante para garantir que o sorteio seja justo e que todos os participantes tenham chances iguais de ganhar.Para
calcular o número de maneiras diferentes de distribuir prêmios, usamos a seguinte fórmula:“`P(n, r) = n! / (n
r)!
“`Onde:* P(n, r) é o número de maneiras de distribuir r prêmios entre n vencedores
- n é o número total de prêmios
- r é o número de vencedores
Por exemplo, se houver 10 prêmios e 3 vencedores, o número de maneiras diferentes de distribuir os prêmios é:“`P(10, 3) = 10! / (103)! = 120“`Isso significa que há 120 maneiras diferentes de distribuir os prêmios entre os 3 vencedores.A
tabela a seguir mostra o número de combinações possíveis para diferentes distribuições de prêmios:| Tipo de prêmio | Número de prêmios | Número de combinações ||—|—|—|| 1º lugar | 1 | 1 || 2º lugar | 1 | 1 || 3º lugar | 1 | 1 || Menção honrosa | 3 | 3 |Como podemos ver na tabela, há apenas uma maneira possível de distribuir o 1º, 2º e 3º lugares, pois há apenas um prêmio de cada tipo.
No entanto, há 3 maneiras possíveis de distribuir as menções honrosas, pois há 3 prêmios deste tipo.
Em essência, a análise combinatória nos capacita a navegar no labirinto das possibilidades, fornecendo uma estrutura para tomar decisões informadas e apreciar a complexidade do mundo ao nosso redor.

